Du 29 au 31 mars 2023 – Petit Amphi, UFR MIM, Metz
Oratrices et orateurs
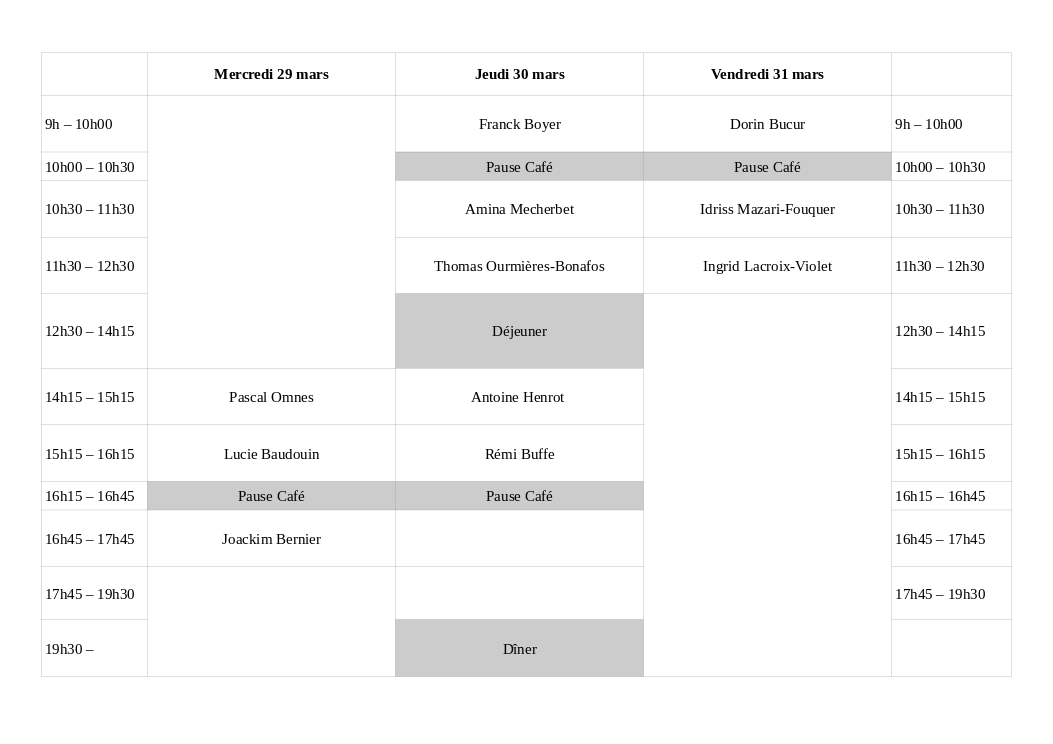
Liste des exposés dans l’ordre chronologique
Lorsqu’un domaine de calcul présente de fortes hétérogénéités (nombreux obstacles, coefficients oscillants), les méthodes d’éléments finis usuelles nécessitent des maillages dont la finesse peut se révéler prohibitive. Les éléments finis multi-échelles sont des méthodes de (Petrov-)Galerkin dans lesquelles les fonctions de base ne sont plus des polynômes mais sont solutions d’équations aux dérivées partielles. Ne connaissant pas en général d’expression analytique pour ces fonctions, elles sont approchées numériquement, par exemple par des éléments finis usuels, ce qui confère l’aspect multi-échelles à la méthode. Nous présentons un cadre de construction de ces méthodes, ainsi qu’une application pour la simulation d’écoulements de fluides visqueux incompressibles en milieu encombré.
Prenons un système en boucle fermée défini par un opérateur de dimension infinie, et des opérateurs bornés d’observation et de contrôle. Supposons que ce système est exponentiellement stable. Le premier objet de cet exposé est de proposer un cadre et une loi d’échantillonnage de la boucle de commande de manière à ne mettre à jour le contrôle du système qu’à des instants pertinents pour conserver la propriété de stabilité exponentielle en boucle fermée. L’approche, basée sur une fonctionnelle de Lyapunov appropriée, permet de démontrer les résultats de caractère bien posé, d’absence de point d’accumulation de la mise à jour et de stabilité attendus. Le cadre proposé englobe en particulier les équations de transport, des ondes, de KdV ou de Schrödinger.
Le second sujet de l’exposé concerne le cas particulier de l’amortissement frontière de l’équation des ondes et des solutions proposées en réponse aux limites liées à l’approche précédente si l’on se confronte à un cadre de contrôle non-borné.
Ces dernières décennies les méthodes de formes normales ont connu d’importants succès pour montrer la stabilité en temps longs des petites solutions d’équations dispersives non-linéaires sur des domaines bornés. Cependant, hormis dans le cas des équations intégrables, ces résultats ne concernent que des solutions très régulières. Cette hypothèse de régularité semble primordiale d’un point de vue technique (afin de compenser les pertes dues aux petits diviseurs) mais, étonnamment, les simulations numériques suggèrent fortement que la stabilité des petites solutions ne devrait pas dépendre de leur régularité. Je vous présenterai quelques résultats récents, obtenus en collaborations avec Benoît Grébert, Gabriel Rivière et Tristan Robert, et allant dans le sens de ces observations numériques.
Dans cet exposé je montrerai comment on peut prouver ou infirmer la contrôlabilité de systèmes paraboliques couplés en étudiant précisément des problèmes de moments. J’illustrerai en particulier l’influence des phénomènes de condensation spectrale dans l’analyse.
L’équation de Transport-Stokes modélise la sédimentation d’une suspension de particules rigides sphériques dans un fluide visqueux en négligeant les effets inertiels du fluide et des particules.
Après avoir rappelé les résultats connus concernant l’existence et unicité de ce modèle, je présenterai des résultats récents obtenus en collaboration avec Franck Sueur concernant l’existence, l’unicité, l’analyticité, la contrôlabilité ainsi que certaines questions ouvertes/en cours d’investigation.
Je parlerai dans une seconde partie d’autres propriétés de ce modèle en rapport avec la stabilité d’une solution stationnaire de type patch. Cette seconde partie est basée sur des travaux en cours en collaboration avec Matthieu Bonnivard.
On s’intéresse au spectre de l’opérateur de Dirac avec des conditions au bord de type masse infinie dans des voisinages tubulaires d’hypersurfaces de l’espace euclidien usuel (de dimension quelconque). On s’intéresse à une description précise du spectre de cet opérateur pour le régime asymptotique dans lequel le voisinage tubulaire devient fin. On démontre l’existence d’un opérateur effectif (posé sur l’hypersurface) qui est responsable dans ce régime de la séparation des valeurs propres. Cet opérateur effectif est de nature géométrique et fait intervenir les courbures de l’hypersurface considérée.
Je commencerai cet exposé en présentant tout d’abord des résultats obtenus en dimension deux pour des guides d’ondes puis j’expliquerai comment on a utilisé cette approche pour traiter une hypersurface compacte sans bord.
Il s’agit d’une série de trois travaux en collaboration avec : W. Borrelli, P. Briet, N. Kerraoui, D. Krejcirik et V. Lotoreichik
Dans cet exposé, nous donnons des bornes supérieures optimales pour les valeurs propres du Laplacien-Neumann pour un domaine convexe (ou plus généralement pour un domaine dont le « profil » a certaines propriétés de convexité). Nous étudions aussi le problème de la borne inférieure, montrant l’existence d’un domaine optimal pour tout
,
parmi les convexes de diamètre donné. Nous donnerons aussi des propriétés qualitatives des domaines optimaux.
Il s’agit d’un travail en collaboration avec Marco Michetti et Beni Bogosel
On s’intéresse à la contrôlabilité d’un système couplant une équation de Stokes à une équation de la chaleur sur une partie de sa frontière. Il s’agit d’un modèle simplifié d’un problème d’interaction fluide-structure modélisant l’écoulement d’un fluide visqueux incompressible à l’intérieur d’une structure élastique modélisée par une équation des plaques amorties. La démonstration est basée sur l’obtention d’inégalités d’interpolation pour les opérateurs elliptiques associés, et une adaptation de la stratégie mise en place par Lebeau et Robbiano dans le contexte de l’équation de la chaleur.
- Dorin Bucur, Autour des inégalités isopérimétriques non locales de type polygonal: Hardy, Riesz, Faber-Krahn
Le problème au départ est l’inégalité de Faber-Krahn sur la première valeur propre du Laplacien avec des conditions de Dirichlet au bord. Des recherches intensives ces dernières années ont mené vers des résultats très fins, comme des versions quantitatives, compétition avec d’autres énergies, valeurs propres d’ordre supérieur, et tout ceci dans le cadre des problèmes à frontière libre de type vectoriel. Pourtant, la version polygonale de cette inégalité, malgré un énoncé très simple, reste complétement ouverte depuis 1947 quand elle a été conjecturée par Polya. Je vais interpréter ce problème à travers des questions (probablement) plus abordables, comme des inégalités isopérimétriques non locales dans la classe des polygones, de type Hardy et Riesz. De plus, je vais discuter la minimalité locale des polygones réguliers et la possibilité de résoudre la conjecture par une approche mixte, en pointant les difficultés théoriques et numériques. Ces résultats sont obtenus dans des travaux conjoints avec Beniamin Bogosel et Ilaria Fragala.
- Idriss Mazari-Fouquer, Fronts de propagation & Jeux à champ moyen : une analyse de la tragédie des communs
Dans ce travail en collaboration avec Z. Kobeissi (INRIA Paris, Institut Bachelier) et D. Ruiz-Balet (Imperial College) nous proposons une analyse d’un problème de pêche optimale du point de vue des jeux à champ moyen. Notre objectif est de mettre en évidence que, d’une part, une pêche trop intensive peut mener à l’extinction de la population de poissons si chaque pêcheur agit de manière à maximiser la quantité qu’il pêche, et, d’autre part que, si les pêcheurs se coordonnaient entre eux, ils pourraient à la fois obtenir une quantité de poissons plus importante qu’en agissant de manière égoïste, tout en garantissant la survie de la population. Mathématiquement, nous utilisons une approche de type front de propagation & jeux à champ moyen: la population suit une équation bistable qui, en l’absence de pêcheurs, admet un unique front de propagation invalide. En décrivant la population de pêcheurs via un modèle de type jeux à champ moyen, nous obtenons un système MFG, dont nous montrons qu’il admet des fronts de propagation de type extinction.
Dans cet exposé, nous nous intéresserons à l’équation de Schrödinger non linéaire. Cette équation possède plusieurs invariants dont la masse et l’énergie. Il est donc intéressant de pouvoir construire des méthodes numériques d’intégration en temps qui, idéalement, préservent la masse, l’énergie et sont d’ordre élevé.
Dans cet exposé, je présenterai deux « généralisations » de la méthode de relaxation, présentée par C. Besse en 2004 pour le cas cubique, qui est une méthode d’ordre 2. Cette méthode est une méthode linéairement implicite, ce qui permet de réduire les coûts de calcul. Les généralisations présentées en conservent le caractère linéairement implicite. La première permet de traiter le cas d’exposants quelconques tout en continuant à préserver la masse et l’énergie et en conservant l’ordre 2. La seconde permet d’obtenir des ordres aussi élevés que voulu tout en continuant de préserver la masse. Cette dernière peut également s’appliquer à toute une classe d’équations dont l’équation de Schrödinger fait partie.