Du 28 au 30 mars 2022 – Amphi 7, FST, Vandœuvre-lès-Nancy
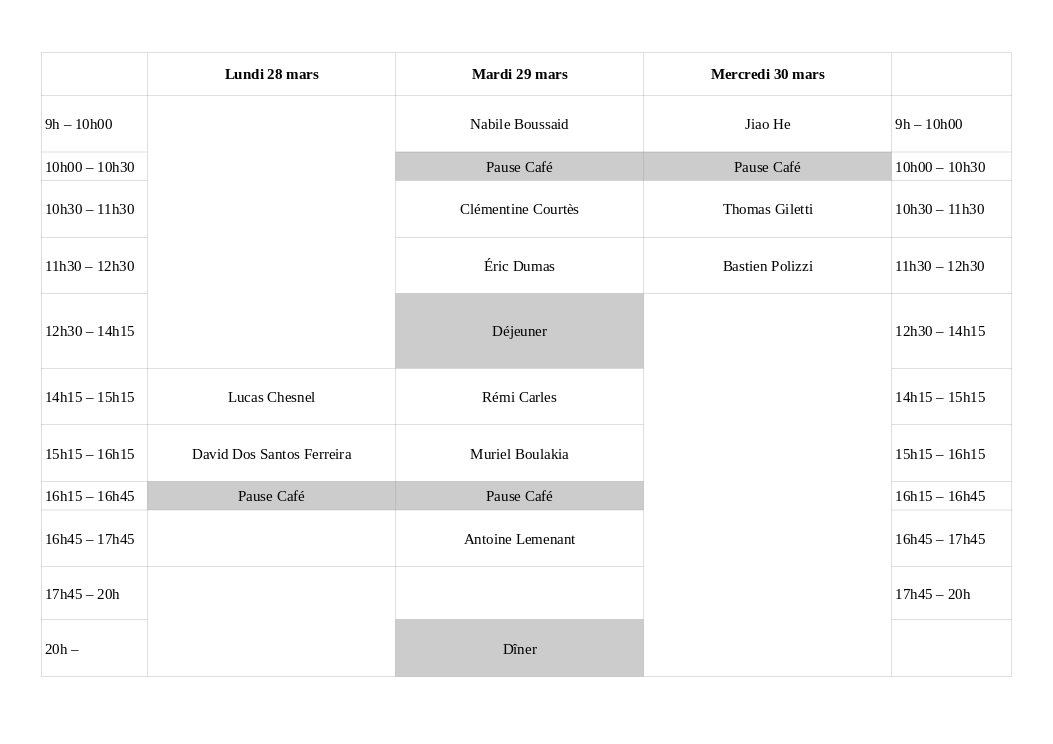
Conférenciers et titres des exposés
Liste des exposés dans l’ordre chronologique
- Lucas Chesnel, Camouflage d’obstacles dans des guides d’ondes acoustiques au moyen de ligaments fins résonants
Nous nous intéressons à la propagation d’ondes dans des guides acoustiques non bornés dans une direction. De manière générale, pour un obstacle donné, l’envoi d’une onde dans la structure génère une réflexion et une transmission caractérisées par des coefficients de diffraction. Le but de la présentation est d’expliquer comment perturber le guide pour faire en sorte que les coefficients de diffraction dans la nouvelle géométrie soient les mêmes que dans la situation de référence sans obstacle. Autrement dit, nous montrons comment rendre l’obstacle invisible. Mathématiquement, l’étude repose sur de l’analyse asymptotique en présence de ligaments fins résonants qui nous permettent de jouer avec des résonances complexes et d’annihiler la diffraction liée à l’obstacle. Il s’agit d’un travail réalisé en collaboration avec J. Heleine et S.A. Nazarov.
- David Dos Santos Ferreira, Sur le problème de Calderón anisotrope dans une classe conforme de produits tordus
Le problème inverse de Calderón concerne l’identifiabilité d’une métrique riemannienne d’une variété compacte à bord à partir de l’opérateur Dirichlet-à-Neumann. Les cas de la dimension 2 et des variétés analytiques sont bien compris mais le problème inverse dans le cas lisse en dimensions supérieures reste ouvert. Une première étape consiste à se restreindre à une classe conforme de métriques afin d’éviter les invariances par isométries, et de chercher l’identifiabilité d’un facteur conforme. La méthode développée par Sylvester et Uhlmann pour résoudre le problème dans la classe conforme de la métrique euclidienne nécessite l’existence de poids limites de Carleman. Des hypothèses de structure sont donc nécessaires sur la métrique, et les métriques tordues avec un facteur euclidien entrent dans cette catégorie. Le problème peut alors se ramener à la construction de quasimodes pour une équation de Helmoltz dans la variété transverse au facteur euclidien et l’étude de la limite haute fréquence de ces quasimodes. Je discuterai d’une construction d’une famille de quasimodes qui sont des distributions lagrangiennes semi-classiques et de leur comportement haute fréquence.
- Nabile Boussaid, Stabilité spectrale d’ondes solitaires pour une équation de Dirac avec une non-linéarité concentrée en un point
Je présenterai un travail en collaboration avec Claudio Cacciapuoti, Raffaele Carlone, Andrew Comech, Diego Noja et Andrea Posilicano où nous considérons une équation de Dirac avec une non-linéarité de type scalaire portée par une impulsion de Dirac. Nous faisons une étude détaillée du spectre du linéarisé autour d’un état stationnaire. Après un résultat d’existence des états stationnaires, je ferai une présentation des résultats généraux sur le spectre essentiel, le noyau et les symétries du spectre. Je m’appliquerai à détailler le spectre discret qui capture toute l’information sur la stabilité ou l’instabilité spectrale. Si le temps le permet, je parlerai des perturbations du modèle.
- Clémentine Courtès, Étude des ondes progressives pour l’équation de Korteweg-de Vries-Kuramoto-Sivashinsky
L’équation de Korteweg-de Vries-Kuramoto-Sivashinsky (KdV-KS) est une équation servant à modéliser l’écoulement d’un film mince sur un plan incliné. Elle possède un terme de dispersion et deux termes de diffusion : un d’ordre 2 et un d’ordre 4. Nous nous intéressons à l’existence de solutions particulières, appelées ondes progressives, pour deux cas dégénérés : (KdV-KS) sans diffusion d’ordre 4 puis (KdV-KS) sans diffusion d’ordre 2.
Il s’agit d’un travail en collaboration avec Frédéric Rousset (LMO, Université Paris Saclay).
Un système d’EDP classique dans l’étude des interactions laser-plasma est le système (bifluide) d’Euler-Maxwell, qui est un sytème hyperbolique quasi-linéaire. Un Ansatz souvent utilisé dans l’asymptotique haute-fréquence repose sur le modèle de Zakharov (couplage non-linéaire Schrödinger-ondes).
Je présenterai une étude de type « optique géométrique » sur le comportement en temps court de solutions rapidement oscillantes de systèmes hyperboliques quasi-linéaires montrant comment des résonances de type espace-temps engendrent des instabilités. Cela limite la validité de l’asymptotique « Zakharov », et explique peut-être les difficultés pour obtenir de bons rendements dans les expériences de fusion nucléaire par confinement inertiel.
C’est un travail en collaboration avec B. Texier (Lyon) et Lu Y. (Nanjing).
On considère l’équation Schrödinger avec non-linéarité logarithmique. La singularité du logarithme à l’origine modifie sensiblement la dynamique. En présence d’un potentiel quadratique, on analyse l’existence et la stabilité des ondes solitaires, qui peuvent présenter des caractéristiques inhabituelles. Les résultats présentés sont issus de travaux avec Guillaume Ferriere d’une part, Chunmei Su d’autre part.
Nous nous intéressons ici à la reconstruction numérique du champ de vitesse et de la pression à partir de mesures de la vitesse sur un sous-domaine. Une méthode numérique basée sur la stabilisation du problème discrétisé par Eléments Finis est introduite et nous présenterons une analyse d’erreur de cette méthode à l’aide de résultats de stabilité sur le problème continu. Des tests numériques viendront illustrer ces résultats et la méthode sera ensuite appliquée à la reconstruction de l’écoulement sanguin dans un vaisseau, tout d’abord pour un problème simplifié où la structure est fixe puis dans le cadre d’un problème d’interaction fluide-structure
Dans cet exposé je présenterai un panorama de quelques problèmes à frontière libre provenant de la mécanique, pour lesquels on étudiera la régularité du minimiseur. Nous verrons que certains de ces problèmes sont en dualité avec des fonctionnelles à discontinuité libre célèbres en calcul des variations telles que la fonctionnelle de Mumford-Shah ou sa généralisation vectorielle (fonctionnelle de Griffith). Les derniers développements de l’exposé proviennent de discussions en cours avec Reza Pakzad, actuellement invité à l’université de Lorraine.
Dans cet exposé je présenterai un modèle mathématique dans un oscillating water column qui est un exemple de Wave Energy Convertor (WEC). Dans cet appareil, le système est décrit par les équations de Saint-Venant avec deux obstacles : le premier est un topographe et le deuxième est une structure flottant sur la surface. D’abord, je présenterai un nouveau modèle qui est un problème de transmission entre la partie à gauche et la partie à droite de la structure où les conditions de transmission dépendent de la dynamique de la structure. Ensuite, nous établissons le caractère bien posé en temps court pour ce nouveau modèle.
Les questions de discrétisation et l’analyse numérique seront aussi évoquées ainsi que les résultats numériques.
Les résultats présentés sont issus de collaborations avec Edoardo Bocchi et Gaston Vergara-Hermosilla.
Dans cet exposé nous aborderons l’étude de certaines équations de réaction-diffusion, comportant une hétérogénéité en temps et en espace mais dépendant d’une variable mobile
avec
. De tels problèmes constituent des modèles simplifiés de dynamique de populations dont l’habitat se déplace, par exemple sous l’influence d’un changement climatique ou l’arrivée de nouveaux prédateurs. On distinguera deux situations selon si l’hétérogénéité intervient dans le terme de réaction ou la diffusion. On s’intéressera à la dichotomie entre extinction et persistance de la solution, ainsi que le cas échant à sa vitesse de propagation asymptotique en temps grand. Les résultats présentés sont issus de collaborations avec Juliette Bouhours, Wonhyung Choi et Jong-Shenq Guo, Gregory Faye et Matt Holzer.
Cet exposé sera dédié à la modélisation et à l’étude d’écosystèmes complexes. Dans ce cadre, les modèles que je présenterai sont basés sur des systèmes d’équations aux dérivées partielles qui permettent de décrire l’évolution de la composition des écosystèmes. Afin d’étudier les dynamiques de ces systèmes, des approches numériques éventuellement complétées par des approches analytiques seront présentées, puis ces résultats seront commentés.
Dans une première partie, je présenterai un modèle qui nous a permis de quantifier l’impact de la récolte sur la productivité d’un biofilm. Puis, si le temps le permet, dans une seconde partie, je présenterai un modèle permettant de quantifier la contribution des mécanismes d’hérédité (épi)génétique en environnement périodique (eg. variations saisonnières).